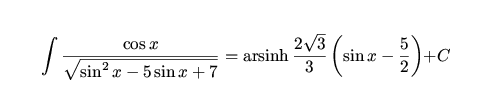Vorlesung im Wintersemester 2003/2004

Computeralgebra

Gegenstand der Vorlesung sind vor allem Algorithmen zum symbolischen Rechnen. Deren Nützlichkeit beschr"ankt sich keinesfalls nur auf Probleme der reinen Mathematik; auch in Anwendungen wie etwa der Computergraphik ist es oft notwendig, sicher zu wissen, ob etwa zwei auf unterschiedliche Weise berechnete Punkte gleich sind; außerdem führt die symbolische Lösung eines Problems oft zu effizienten numerischen Algorithmen zur Lösung konkreter Einzelfälle.

In den Übungen, die sich speziell auch an Lehramtskandidaten wenden, steht der Umgang mit Computeralgebrasystemen im Vordergrund; dort soll es nicht nur um algebraische Algorithmen gehen, sondern beispielsweise auch um den Einsatz von Computeralgebrasystemen zur Visualisierung mathematischer Sachverhalte. Lehramtskandidaten können hier den nach ihrer Prüfungsordnung notwendigen Schein für eine Übung am Rechner erwerben.

Themen

Wozu Computeralgebra

Erstes Thema sind die grundlegenden Unterschiede zwischen numerischem, exaktem und symbolischem Rechnen. Je nach Anwendung hat jeder der drei Zugänge seine Vor- und Nachteile, und oft hängt die Lösbarkeit eines Problems davon ab, daß man den richtigen gewählt hat. Die "großen" Computeralgebrasysteme wie Maple, MuPad und Mathematica unterstützen allesamt jede der drei Methoden.

Datenstrukturen der Computeralgebra

Da es sich um eine mathematische Vorlesung handelt, werde ich die Vielzahl möglicher Datenstrukturen, die in Computeralgebrasystemen verwendet werden, auch nicht annähernd vollständig abhandeln; stattdessen beschränke ich mich auf einige fundamentale Techniken, anhand derer insbesondere auch klar wird, daß ein Computeralgebrasystem gelegentlich eine ganz andere Aufgabe löst als die, die der naive Anwender im Sinn hatte: So können Computeralgebrasysteme einerseits scheinbar mühelos Integrale wie

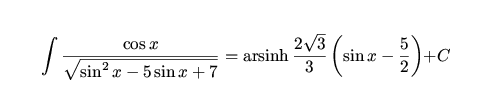
ausrechnen und oft sogar nichtlineare Gleichungssysteme lösen, geben aber andererseits gelegentlich bei einfachen linearen Gleichungssystemen eine falsche oder zumindest unvollständige Lösung an und haben Probleme mit der Anwendung von so einfachen Regeln wie sin² x + cos²x = 1.

Außerdem geht es in diesem Kapitel um grundsätzliche Unentscheidbarkeitsfragen, die jedem Computeralgebrasystem Grenzen setzen: Es gibt keine endliche Datenstruktur zur Beschreibung beliebiger reeller Zahlen.

Der Euklidische Algorithmus

Der Euklidischen Algorithmus zur Bestimmung des größten gemeinsamen Teilers wird wohl (fast) jedem geläfig sein, ist aber in der Praxis, insbesondere wenn es um den ggT von Polynomen geht, keineswegs so unproblematisch, wie man auf den ersten Blick meinen möchte. Bereits hier macht sich eines der Grundprobleme der Computeralgebra bemerkbar: Selbst bei Problemen mit kleinen Ausgangsdaten und kleinen Ergebnissen können riesige Zwischenresultate auftreten. Aus diesem Grund muß der Algorithmus für eine effiziente Anwendung modifiziert werden, und die Strategien, die man hier anwendet, werden sich auch bei komplizierteren und interessanteren Problemen als nützlich erweisen.

Faktorisierung von Polynomen

Das Ausmultiplizieren eines Produkts von Polynomen ist bei hohen Graden oder einer großen Anzahl von Faktoren zwar aufwendig, erfordert aber keinerlei mathematische Ideen. Für die Zerlegung eines Polynoms in Faktoren dagegen gibt es keinen offensichtlichen Ansatz, obwohl auch diese Zerlegung beispielsweise für die Nullstellenbestimmung sehr nützlich ist. Die Computeralgebra hat verschiedene Algorithmen entwickelt, die dieses Problem effizient lösen können.

Symbolische Integration

Schon die möglcherweise aus der Analysis bekannte Integration rationaler Funktionen via Partialbruckzerlegung ist nicht wirklich algorithmisch, da der Nenner in h"ochstens quadratische Faktoren zerlegt werden muß, was nur für hinreichends spezielle Polynome algorithmisch effizient möglich ist; Integrale transzendenter Funktionen werden meist mit ad hoc Methoden behandelt. Tatsächlich gibt es aber eine ganze Reihe von Verfahren, die teilweise bis ins 19. Jahrhundert zur¨ckgehen, mit denen man für große Klassen von Funktionen nicht nur Stammfunktionen konstruieren kann, sondern mit denen man gegebenenfalls auch beweisen kann, daß es keine Stammfunktion gibt, die sich durch gewisse vorgegebene Funktionen ausdrücken läßt: Beispielsweise kann die Stammfunktion von exp(-x²) nicht durch Grundrechenarten, Wurzeln, Exponentialfunktionen, Logarithmen, trigonometrische Funktionen und deren Umkehrfunktionen ausgedrückt werden.

Nichtlineare Gleichungssysteme

Lineare Gleichungssysteme lassen sich vor allem deshalb so einfach lösen, weil ihre Nullstellenmenge eine lineare Stuktur hat. Im Nichtlinearen gibt es nur noch selten Strukturen, so daß es hier zumindest im Fall einer unendlichen Lösungsmenge nur daum gehen kann, das Gleichungssystem in eine möglichst einfache Form überzuführen. Bei endlicher Lösungsmenge möchte man diese natürlich explizit angeben. Für beide Aufgaben stellt die Computeralgebra zwei Arten von Algorithmen zur Verfügung: Die schon im 19. Jahrhundert bekannten Resultantenmethoden, die heute bei der Bewegungsplanung von Robotern eine große Rolle spielen, und die etwa 35 Jahre alten Standardbasen oder Gröbnerbasen, die durch Kombination der Ideen des Gauß-Algorithmus und des Euklidischen Algorithmus auch nichtlineare Gleichungssysteme auf eine Art Treppengestalt bringen können.

Exaktes Rechnen mit reellen Zahlen

Im allgemeinen ist nicht entscheidbar, ob zwei reelle Ausdrücke dieselbe Zahl darstellen oder nicht. Es gibt aber einen relativ großen Teilkörper von R, in dem man exakt rechnen und Gleichheit algorithmisch entscheiden kann. Dies spielt beispielsweise eine große Rolle in einigen Teilen der Computergraphik, wo man mit Sicherheit wissen muß, ob zwei Schnittpunkte gleich sind oder nicht.

Voraussetzungen: Grundkenntnisse der linearen Algebra und Analysis.

Hörerkreis: Für den integrierten Studiengang Mathematik und Informatik kann diese Vorlesung bei entsprechender Vertiefung für das Spezialgebiet Algebra gewählt werden oder aber für das Fach "Brücke", falls Computeralgebra entweder für das Vertiefungsfach oder das Anwendungsgebiet nützlich ist.

Lehramtskandidaten können, wie bereits erwähnt, hier der vorgeschriebenen Schein über eine Übung am Rechner erwerben.

Für Technische Informatiker und Wirtschaftsinformatiker kann die Computeralgebra eventuell als Ergänzung interessant sein.

Literatur: Eine kommentierte Literaturliste in Postskript ist hier zu finden. Die dort aufgeführten Büucher decken natürlich ein Vielfaches des Stoffs ab, der in einer einsemestrigen Vorlesung behandelt werden kann.